You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
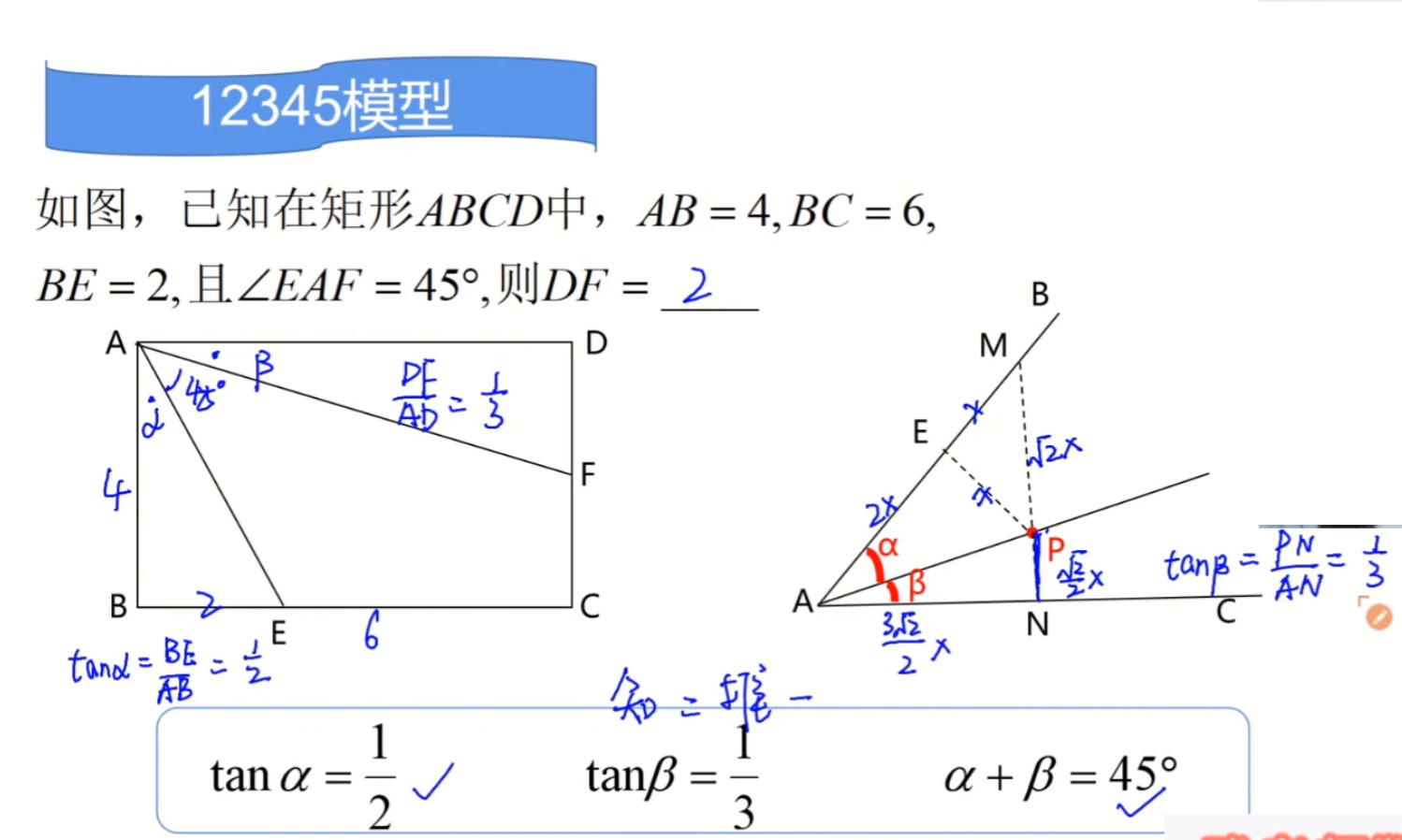
**结论**:
|
|
|
|
|
|
$tan \alpha=\frac{1}{2},tan \beta=\frac{1}{3},\alpha+\beta=45^{\circ}$
|
|
|
|
|
|
|
|
|
|
|
|
利用结论:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
设$\angle BAE=\angle \alpha,\angle FAD=\angle \beta$
|
|
|
|
|
|
|
|
|
|
|
|
$\because BE=2,AB=4$
|
|
|
|
|
|
$\large \therefore \frac{BE}{AB}=\frac{2}{4}=\frac{1}{2}=tan \alpha$
|
|
|
|
|
|
|
|
|
|
|
|
双$\because \alpha+ \beta=45^{\circ}$
|
|
|
|
|
|
根据结论:$\frac{DF}{AD}=\frac{1}{3} $
|
|
|
|
|
|
$\therefore DF=2$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
**证明**:
|
|
|
|
|
|
绘制右侧的图形,$\angle \alpha +\beta=45^{\circ}$
|
|
|
|
|
|
|
|
|
|
|
|
取角分线上任意一点$P$,向$AB,AC$引垂线,构造直角三角形,同时,延长$NP$交$AB$与$M$。
|
|
|
|
|
|
|
|
|
|
|
|
这样就有了好多个直角三角形,计算起来就容易了:
|
|
|
|
|
|
|
|
|
|
|
|
$\because tan\alpha=\frac{1}{2}$
|
|
|
|
|
|
设$EP=x$,则$AE=2x$
|
|
|
|
|
|
|
|
|
|
|
|
$\because \angle ANM$是引垂线引出的直角三角形,$\angle NAB=45^{\circ}$
|
|
|
|
|
|
|
|
|
|
|
|
$\therefore \angle AMN=45^{\circ}$
|
|
|
|
|
|
$\therefore EM=EP=x$
|
|
|
|
|
|
$PM=\sqrt{2}x,AM=3x$
|
|
|
|
|
|
|
|
|
|
|
|
再利用等腰直角三角形的边长关系,得到
|
|
|
|
|
|
|
|
|
|
|
|
$AN=MN$
|
|
|
|
|
|
|
|
|
|
|
|
$\because 2 AN^2=(3x)^2$
|
|
|
|
|
|
$AN=\sqrt{\frac{(3x)^2*2}{2*2}}=\frac{3\sqrt{2}}{2}x$
|
|
|
|
|
|
|
|
|
|
|
|
$\therefore PN=\frac{3\sqrt{2}}{2}x-\sqrt{2}x=\frac{\sqrt{2}}{2}x$
|
|
|
|
|
|
|
|
|
|
|
|
$\therefore tan \beta=\frac{PN}{AN}=\frac{1}{3}$
|
|
|
|
|
|
|
|
|
|
|
|
**证毕**
|