You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
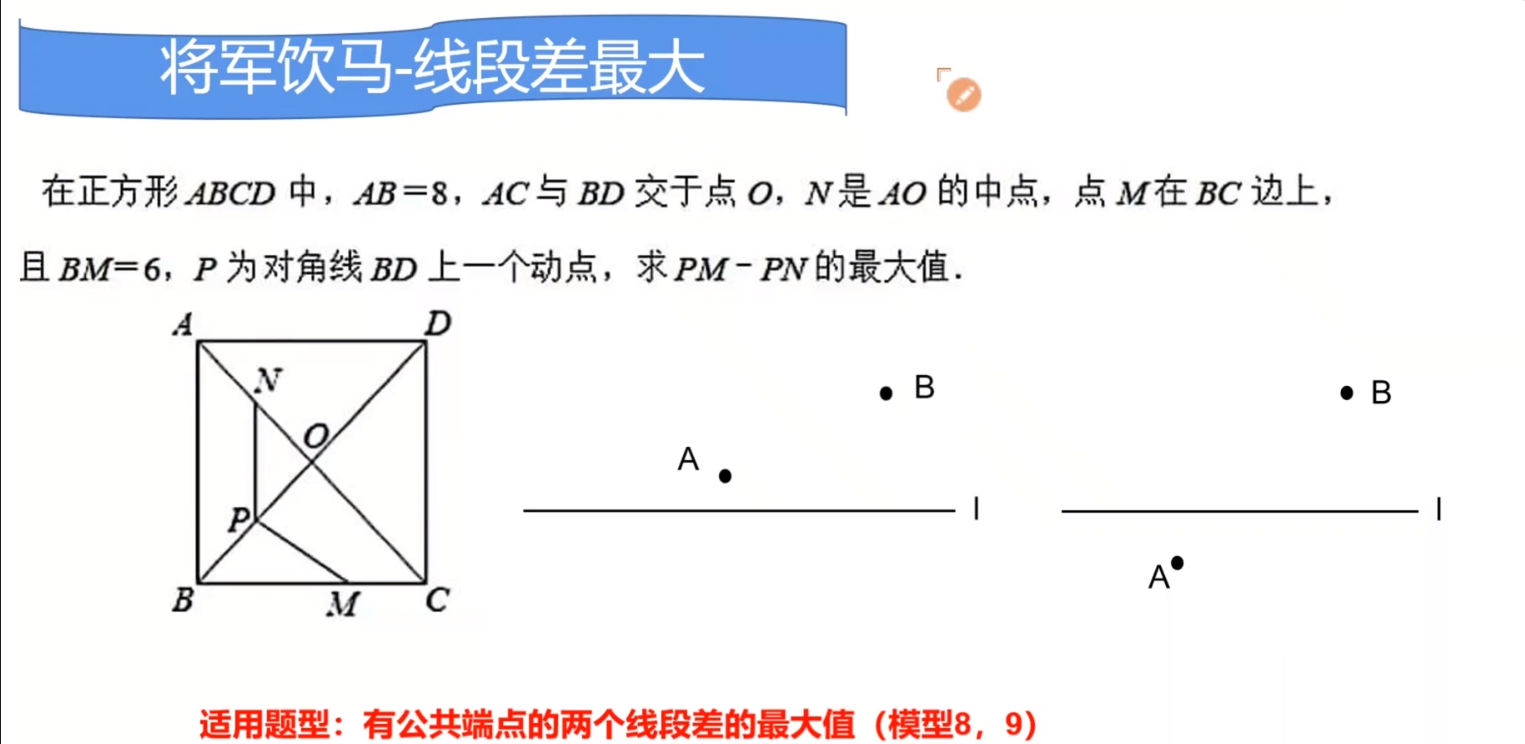
**前导知识**
|
|
|
|
|
|
$P,A,B$三个点之间的关系,是
|
|
|
|
|
|
- 要么共线
|
|
|
|
|
|
- 要么不共线
|
|
|
|
|
|
|
|
|
|
|
|
>共线时
|
|
|
|
|
|
不能构成一个三角形
|
|
|
|
|
|
- 如果$P$在$A,B$中间,则$|PA-PB|$就是两条线段的差值
|
|
|
|
|
|
- 如果$P$在$A,B$的延长线上,则$AB=|PA-PB|$
|
|
|
|
|
|
|
|
|
|
|
|
>不共线时
|
|
|
|
|
|
可以构成一个三角形,必须符合三角形的三边关系:$PA+PB>AB>|PA-PB|$
|
|
|
|
|
|
|
|
|
|
|
|
综上所述,我们知道,**只有在三点共线时,上面的$AB$才可以取到等号**,(不共线时,必然取不到等号)。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
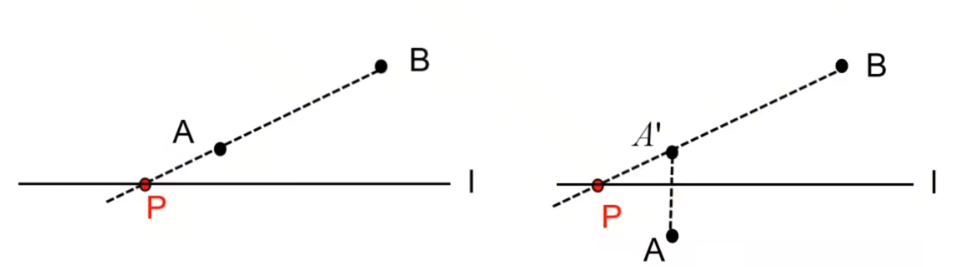
$A,B$都在河一侧,连接$A,B$延长交河于$P$点,则此时
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如果不在同一侧呢?那么也简单,就是对河取一下对称点$A'$,连接$BA'$就行了。
|
|
|
|
|
|
|
|
|
|
|
|
**本题解析**
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
求两条线段的差值最大值,需要两个端点在河的同侧,那么针对$N$关于$BD$做对称点$N'$,因为$ABCD$是正方形,所以$N'$必然落在$AC$上。
|
|
|
|
|
|
|
|
|
|
|
|
延长$MN'$交$BD$于$P'$,也就是$P$这个动点,走到$P'$这个位置上时,$PN$也就是$P'N'$的长度,$PM$的长度也就是$P'M$的长度,三点共线时,两条线段的差最大,最大值就是$P'M-P'N=MN'$
|
|
|
|
|
|
|
|
|
|
|
|
$\because BM=6,BC=8$
|
|
|
|
|
|
$\therefore MC=2$
|
|
|
|
|
|
$\therefore MN'=2$
|