You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
|
|
|
### 将军饮马
|
|
|
|
|
|
|
|
|
|
|
|
#### 模型3
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
**本题由1,2升级而来,不再是两静一定,而是两动一定了!!**
|
|
|
|
|
|
|
|
|
|
|
|
但是很显然,它符合将军饮马问题的基本条件,就是 <font color='red' size=4><b>有公共端点的,两个线段和的最小值</b></font>
|
|
|
|
|
|
|
|
|
|
|
|
那该怎么做呢?
|
|
|
|
|
|
|
|
|
|
|
|
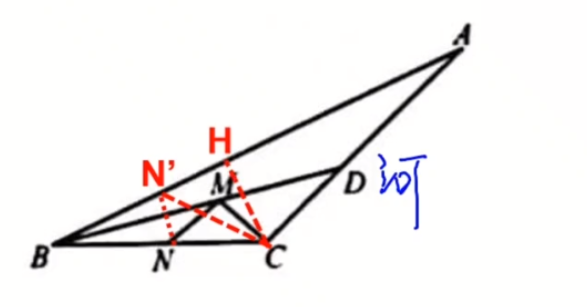
答:先不管什么$N$是不是动点,我们直接按模型$2$来做,视$N$为定点。则有关于河$BD$做出对称点$N'$,连接$C \sim N'$,则$CN'$就是答案。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
但问题是$N$是动点,$N'$也是动点,没法求啊~
|
|
|
|
|
|
|
|
|
|
|
|
我们再来看一下条件,有一个$BD$是角平分线的条件,所以$N$关于角平分线的对称点,**一定** 是在$BA$上!
|
|
|
|
|
|
|
|
|
|
|
|
问题就进一步转化为 **求$C$到$AB$上某一个点的距离最短**,那不就是垂线段最短吗?
|
|
|
|
|
|
|
|
|
|
|
|
所以,从$C$引垂线到$AB$,垂足为$H$,求出$HC$就是答案。
|
|
|
|
|
|
|
|
|
|
|
|
因为知道三角形面积$S_{\triangle ABC}=1/2 \times AB \times CH$
|
|
|
|
|
|
|
|
|
|
|
|
$18=1/2 \times 12 \times CH$
|
|
|
|
|
|
|
|
|
|
|
|
$\therefore CH=3$
|