You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
49 lines
1.7 KiB
49 lines
1.7 KiB
|
2 years ago
|
|
||
|
|
|
||
|
|
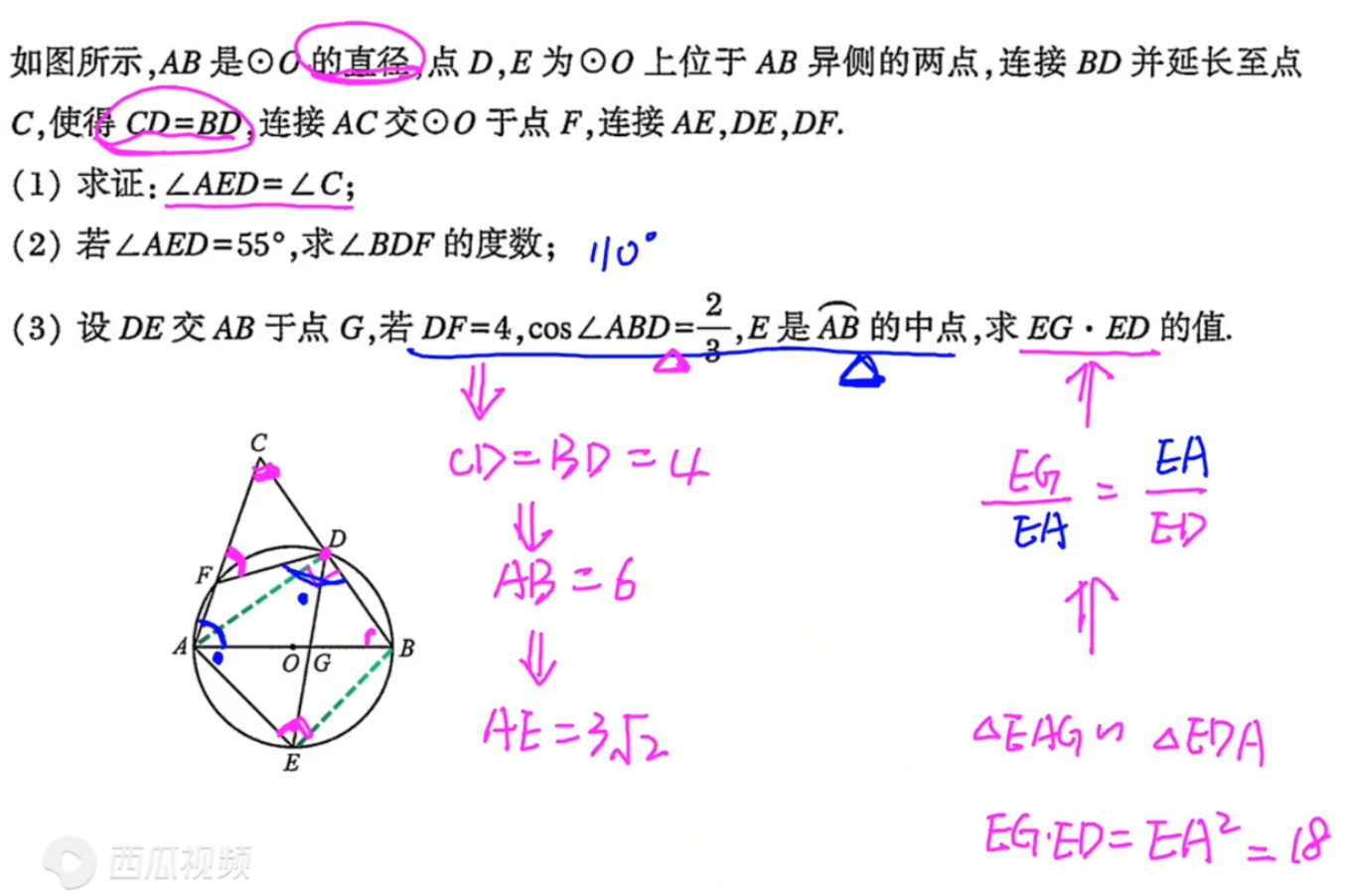
### 一、第一问
|
||
|
|
$\because$ 圆中同弧所对的圆周角相等
|
||
|
|
$\therefore$ $\angle AED=\angle ABD$ ①
|
||
|
|
|
||
|
|
连接$AD$, $\because \angle ADB$是直径$AB$所对的圆周角,$\therefore \angle ADB=90^{\circ}$
|
||
|
|
又 $\because D$是$BC$中点,所以$\triangle ADB \cong \triangle ADC$
|
||
|
|
$\therefore \angle ABD = \angle ACB$ ②
|
||
|
|
|
||
|
|
联立 ① ②, $\therefore \angle AED=\angle C$
|
||
|
|
|
||
|
|
### 二、第二问
|
||
|
|
$\because \angle AED=55^{\circ}$
|
||
|
|
$\therefore \angle ABC=\angle C=55^{\circ}$
|
||
|
|
$\therefore \angle BAC=180^{\circ}-55^{\circ}-55^{\circ}=70^{\circ}$
|
||
|
|
根据 <font color='blue' size=4><b>圆的内接四边形对角互补</b></font>,$\therefore \angle BDF=110^{\circ}$
|
||
|
|
|
||
|
|
### 三、第三问
|
||
|
|
看到线段乘积,考虑找到相似三角形
|
||
|
|
$$\large \frac{EG}{?}=\frac{?}{ED}$$
|
||
|
|
考虑$\triangle EAG \sim \triangle EAD$
|
||
|
|
|
||
|
|
如何证明呢?
|
||
|
|
有一个公共角$\angle AED$
|
||
|
|
还需要再找一个角:
|
||
|
|
因为$E$是 $\overset{{\frown}}{AB}$ 的中点,
|
||
|
|
$\therefore \angle ADE=\angle BAE$
|
||
|
|
|
||
|
|
$\therefore \triangle EAG \sim \triangle EAD$
|
||
|
|
|
||
|
|
|
||
|
|
$$\large \frac{EG}{AE}=\frac{AE}{ED}$$
|
||
|
|
$\Rightarrow$ $EG*ED=AE^2$
|
||
|
|
|
||
|
|
$AE$长度如何求解呢?
|
||
|
|
$\because \angle AFD+\angle ABD=180^{\circ}$
|
||
|
|
$\because \angle AFD+\angle CFD=180^{\circ}$
|
||
|
|
$\therefore \angle ABD=\angle CFD$
|
||
|
|
因为有第一问的结论,所以$\triangle DCF$是等腰三角形,$CD=DF=BD=4$
|
||
|
|
|
||
|
|
$\because cos\angle ABD=\frac{2}{3}$
|
||
|
|
$\large \therefore \frac{BD}{AB}=\frac{2}{3}$
|
||
|
|
$\therefore AB=6$
|
||
|
|
|
||
|
|
$\because \triangle ABE$是等腰直角三角形
|
||
|
|
$\therefore AE=3\sqrt{2}$
|
||
|
|
|
||
|
|
$\therefore EG*ED=(3\sqrt{2})^2=18$
|