You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
24 lines
910 B
24 lines
910 B
|
2 years ago
|
|
||
|
|
|
||
|
|
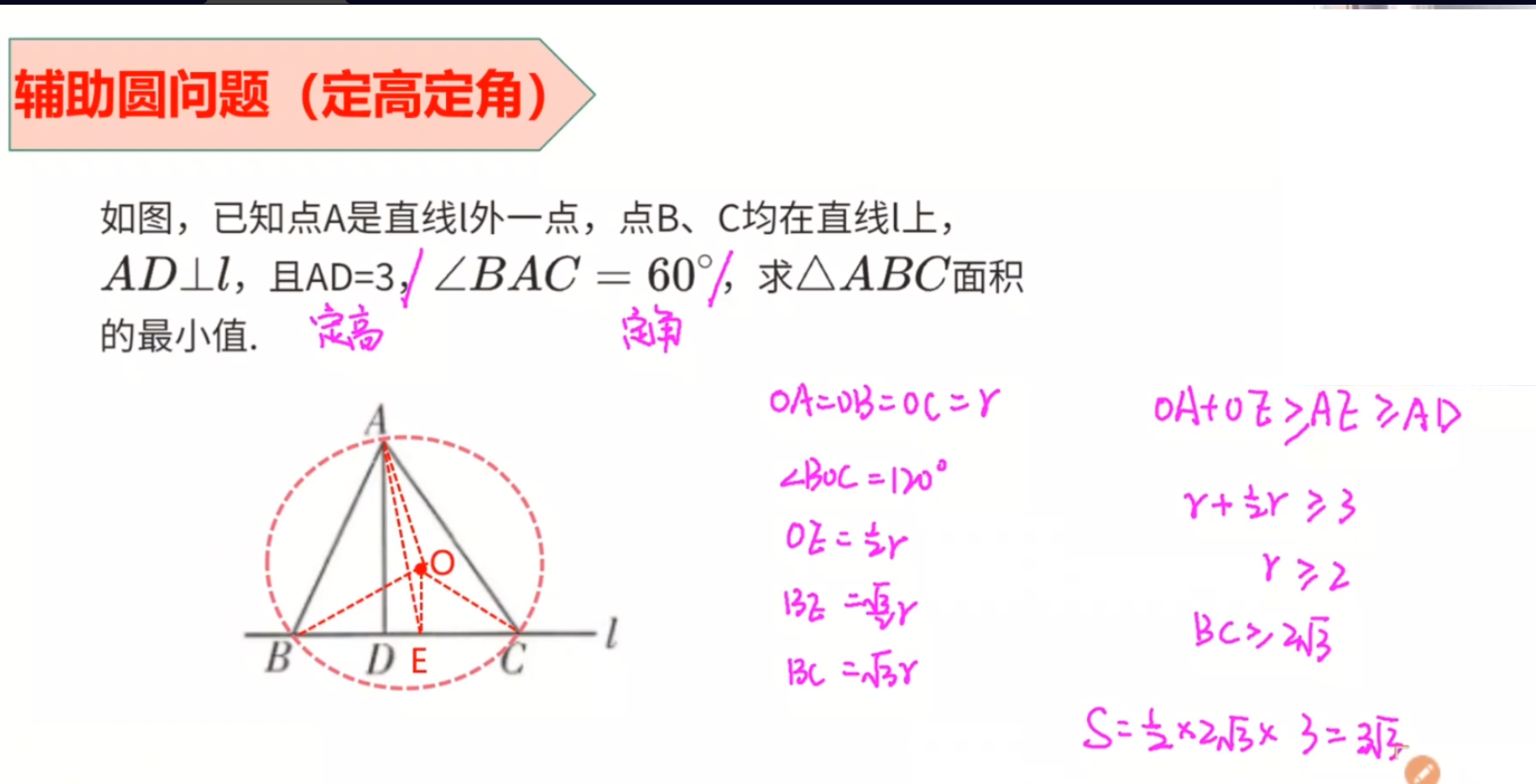
- 定角:则做$\triangle BAC$的外接圆
|
||
|
|
- 既然都有了外接圆,就需要有圆心有半径,设圆心$O$,连接$OA=OB=OC=r$
|
||
|
|
- $\because \angle BAC=60^{\circ}$
|
||
|
|
$\therefore \angle BOC=120 ^ \circ$
|
||
|
|
- 从$O$引$BC$垂线$OE$交$BC$于$E$点
|
||
|
|
则$\angle EOC=60 ^{\circ},\angle ECO=30 ^{\circ}$
|
||
|
|
|
||
|
|
$\therefore OE=\frac{1}{2}r,EC=\frac{\sqrt{3}}{2}r$
|
||
|
|
|
||
|
|
$\therefore BC=\sqrt{3}r$
|
||
|
|
|
||
|
|
预求$\triangle ABC$的面积最小值,面积表示为
|
||
|
|
$\frac{1}{2} BC \times AD$
|
||
|
|
其中$AD$为定高,等于$3$,所以$BC$最小,则面积最小。
|
||
|
|
也就是$\sqrt{3}r$最小即可,也就是$r$最小。
|
||
|
|
|
||
|
|
$OA+OE>=AE>=AD$
|
||
|
|
$\therefore r+\frac{1}{2}r>=3$
|
||
|
|
$\therefore r>=2$
|
||
|
|
$\therefore BC>=2\sqrt{3}$
|
||
|
|
$S=\frac{1}{2}\times 2\sqrt{3}\times 3=3\sqrt{3}$
|