You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
(1)
|
|
|
|
|
|
将三个点代入方程,求解方程组
|
|
|
|
|
|
$$
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
0=a(-1)^2-b+c & \\
|
|
|
|
|
|
0=9a+3b+c & \\
|
|
|
|
|
|
c=-3
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
|
|
|
|
|
|
整理:
|
|
|
|
|
|
$$
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
a-b-3=0 & \\
|
|
|
|
|
|
3a+b-1=0 & \\
|
|
|
|
|
|
c=-3
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$$ \Rightarrow
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
a=1& \\
|
|
|
|
|
|
b=-2& \\
|
|
|
|
|
|
c=-3
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
即$y=x^2-2x-3$
|
|
|
|
|
|
|
|
|
|
|
|
顶点$D$的坐标,根据顶点坐标公式:
|
|
|
|
|
|
|
|
|
|
|
|
$$
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
x=-\frac{b}{2a} & \\
|
|
|
|
|
|
y=\frac{4ac-b^2}{4a} &
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
|
|
|
|
|
|
$$ \Rightarrow
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
x=1 & \\
|
|
|
|
|
|
y=-4 &
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
|
|
|
|
|
|
---
|
|
|
|
|
|
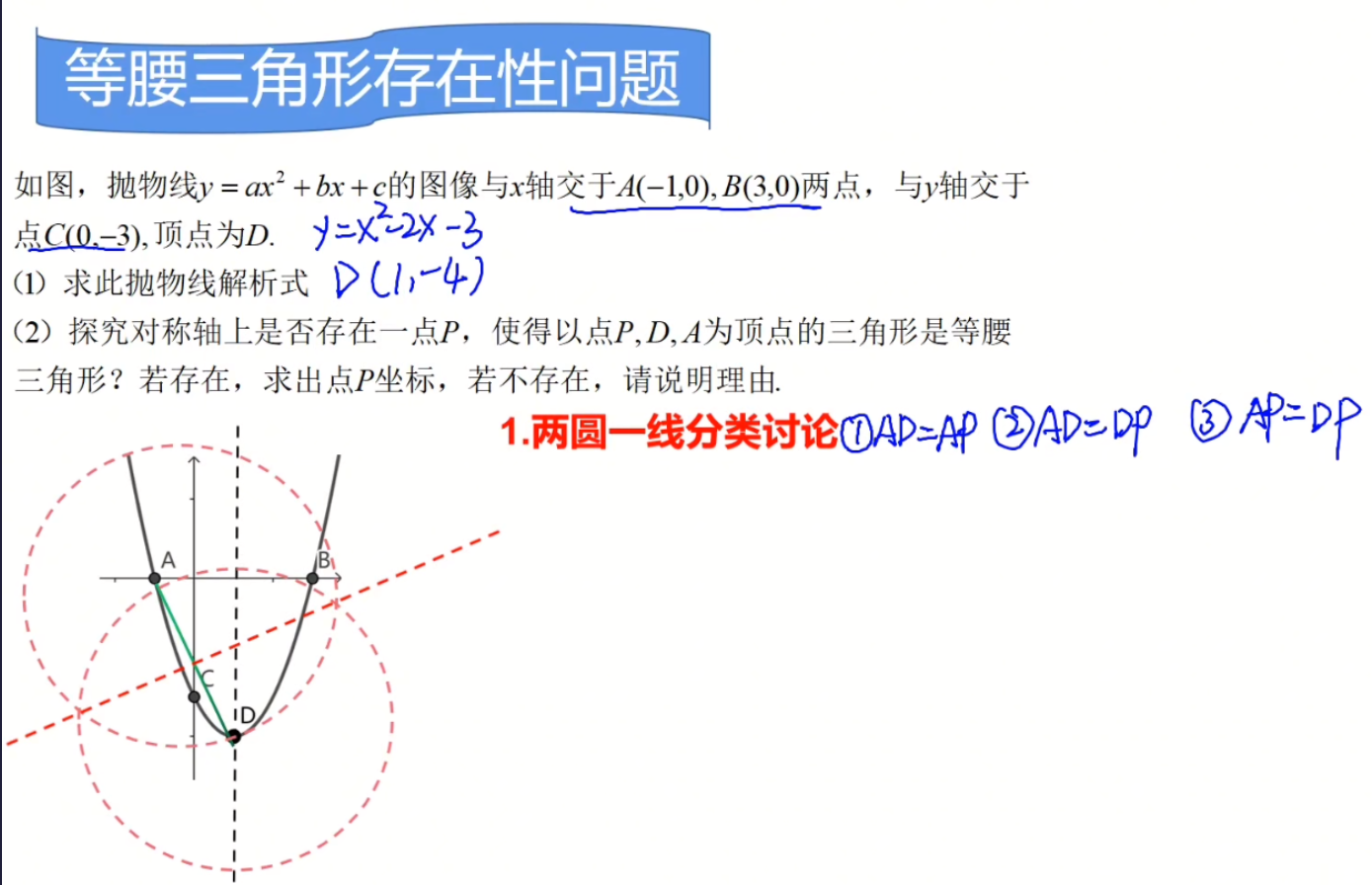
**重点是第二问**:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
因为是等腰三角形的情况共三种,需要分情况讨论:
|
|
|
|
|
|
- $AD=AP$ 在以$A$为圆心,以$AD$长为半径的圆对称轴的交点上
|
|
|
|
|
|
- $AD=DP$ 在以$D$为圆心,以$AD$长为半径的圆对称轴的交点上
|
|
|
|
|
|
- $AP=DP$ 在$AD$垂直平分线与对称轴的交点上
|
|
|
|
|
|
|
|
|
|
|
|
有两种方法,几何法和代数法,分别来计算一下:
|
|
|
|
|
|
|
|
|
|
|
|
#### 几何法
|
|
|
|
|
|
- $AD=AP$ 时,$P$点坐标就是$D$关于$X$轴的对称点,$P(1,4)$
|
|
|
|
|
|
- $AD=DP$ 时,利用勾股定理,可以求解$AD$长度,也就是$DP$长度=$\sqrt{(-1-1)^2+(-4)^2}=2\sqrt{5}$,$P_2=({-1,2\sqrt{5}-4})$
|
|
|
|
|
|
|
|
|
|
|
|
<font color='red' size=4><b>注意</b></font>
|
|
|
|
|
|
这里非常容易丢失一组解!也可能是以$D$为圆心的圆与对称轴的下方交点! 即$P_3=(-4-2\sqrt{5})$
|
|
|
|
|
|
|
|
|
|
|
|
垂直平分线的交点:
|
|
|
|
|
|
此时$AP=PD$
|
|
|
|
|
|
设 上面一小段为$m$
|
|
|
|
|
|
$(4-m)^2=m^2+2^2 \Rightarrow $
|
|
|
|
|
|
$16-8m+m^2=m^2+4$
|
|
|
|
|
|
$m=\frac{3}{2}$
|
|
|
|
|
|
|
|
|
|
|
|
$P_4(1,-\frac{3}{2})$
|
|
|
|
|
|
#### 代数法
|
|
|
|
|
|
|
|
|
|
|
|
- 表示点
|
|
|
|
|
|
$A(-1,0),D(1,-4),P(1,t)$
|
|
|
|
|
|
- 表示边
|
|
|
|
|
|
利用两点间距离公式 $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
|
|
|
|
|
|
分别计算$AD^2,AP^2,DP^2$,就可以免去开根号了
|
|
|
|
|
|
|
|
|
|
|
|
- 列方程求解
|
|
|
|
|
|
$AD^2=4+16=20$
|
|
|
|
|
|
$AP^2=4+t^2$
|
|
|
|
|
|
$DP^2=(t+4)^2$
|
|
|
|
|
|
|
|
|
|
|
|
三个方程式分别联立成三个方程组:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$$
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
4+t^2=20 & ① \\
|
|
|
|
|
|
4+t^2=t^2+8t+16 & ② \\
|
|
|
|
|
|
(t+4)^2=20 & ③
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
|
|
|
|
|
|
① $t=4$ (根据题意舍掉$-4$)
|
|
|
|
|
|
② $t=-\frac{3}{2}$
|
|
|
|
|
|
③ $t=\pm2\sqrt{5}-4$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|