|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
(1) 将三个点代入二次函数,得到一个二元一次方程组,求解即可求出$b,c$
|
|
|
|
|
|
|
|
|
|
|
|
$$
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
0=-1-b+c & \\
|
|
|
|
|
|
3=-4+2b+c & \\
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
$\therefore a=-1,b=2,c=3,方程:y=-x^2+2x+3$
|
|
|
|
|
|
交$y$轴于点$C$,则$x=0,y=3$ $\therefore C坐标(0,3)$
|
|
|
|
|
|
$D$点坐标可求:
|
|
|
|
|
|
$x_d=-\frac{b}{2a}=\frac{2}{2}=1,y_d=\frac{4ac-b^2}{4a}=4$
|
|
|
|
|
|
|
|
|
|
|
|
$AB$的直线方程也很好求:
|
|
|
|
|
|
$y=kx+b$
|
|
|
|
|
|
$$
|
|
|
|
|
|
\large \left\{\begin{matrix}
|
|
|
|
|
|
0=-k+b& \\
|
|
|
|
|
|
3=2k+b&
|
|
|
|
|
|
\end{matrix}\right.
|
|
|
|
|
|
$$
|
|
|
|
|
|
$\therefore k=1,b=1,y=x+1$
|
|
|
|
|
|
|
|
|
|
|
|
---
|
|
|
|
|
|
**重点是第二问**
|
|
|
|
|
|
|
|
|
|
|
|
由于没有说明$A,C,M$哪个顶点是直角顶点,需要分类讨论:
|
|
|
|
|
|
|
|
|
|
|
|
- $A$是直角顶点
|
|
|
|
|
|
此时,过$A$点引$AC$的垂线
|
|
|
|
|
|
- $C$是直角顶点
|
|
|
|
|
|
此时,过$C$点引$AC$的垂线
|
|
|
|
|
|
- $M$是直角顶点
|
|
|
|
|
|
此时,以$AC$为直径画圆,此圆与$y$轴有两个交点
|
|
|
|
|
|
|
|
|
|
|
|
#### 几何法
|
|
|
|
|
|
1. $AM_1$需要做相似三角形,通过比例关系来求解
|
|
|
|
|
|
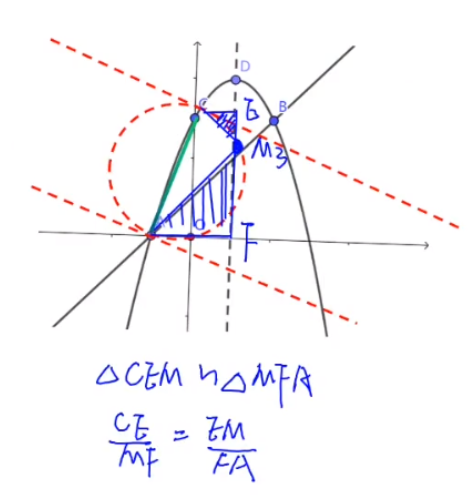
$\triangle AM_1F \sim \triangle CEA$
|
|
|
|
|
|
$\frac{CE}{AF}=\frac{AE}{M_1F}$
|
|
|
|
|
|
$1/m=3/2$ $\Rightarrow m=\frac{2}{3}$
|
|
|
|
|
|
$\therefore M1(1,-\frac{2}{3})$
|
|
|
|
|
|
2. 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
#### 代数法
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
- 当$A$为直角顶点时:
|
|
|
|
|
|
$AC^2+AM^2=CM^2$
|
|
|
|
|
|
$10+t^2+4=t^2-6t+10$
|
|
|
|
|
|
$t=-\frac{2}{3}$
|
|
|
|
|
|
$\therefore M(1,-\frac{2}{3})$
|
|
|
|
|
|
|
|
|
|
|
|
- 当$C$为直角顶点时:
|
|
|
|
|
|
$AC^2+CM^2=AM^2$
|
|
|
|
|
|
$10+t^2-6t+10=t^2+4$
|
|
|
|
|
|
$t=\frac{8}{3}$
|
|
|
|
|
|
$\therefore M(1,\frac{8}{3})$
|
|
|
|
|
|
|
|
|
|
|
|
- 当$M$为直角顶点时:
|
|
|
|
|
|
$AC^2=AM^2+CM^2$
|
|
|
|
|
|
$10=t^2+4+t^2-6t+10$
|
|
|
|
|
|
$t^2-3t+2=0$
|
|
|
|
|
|
$t=2,t=1$
|
|
|
|
|
|
$\therefore M(1,2)$ 或 $M(1,1)$
|