You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
45 lines
1.1 KiB
45 lines
1.1 KiB
|
2 years ago
|
|
||
|
|
|
||
|
|
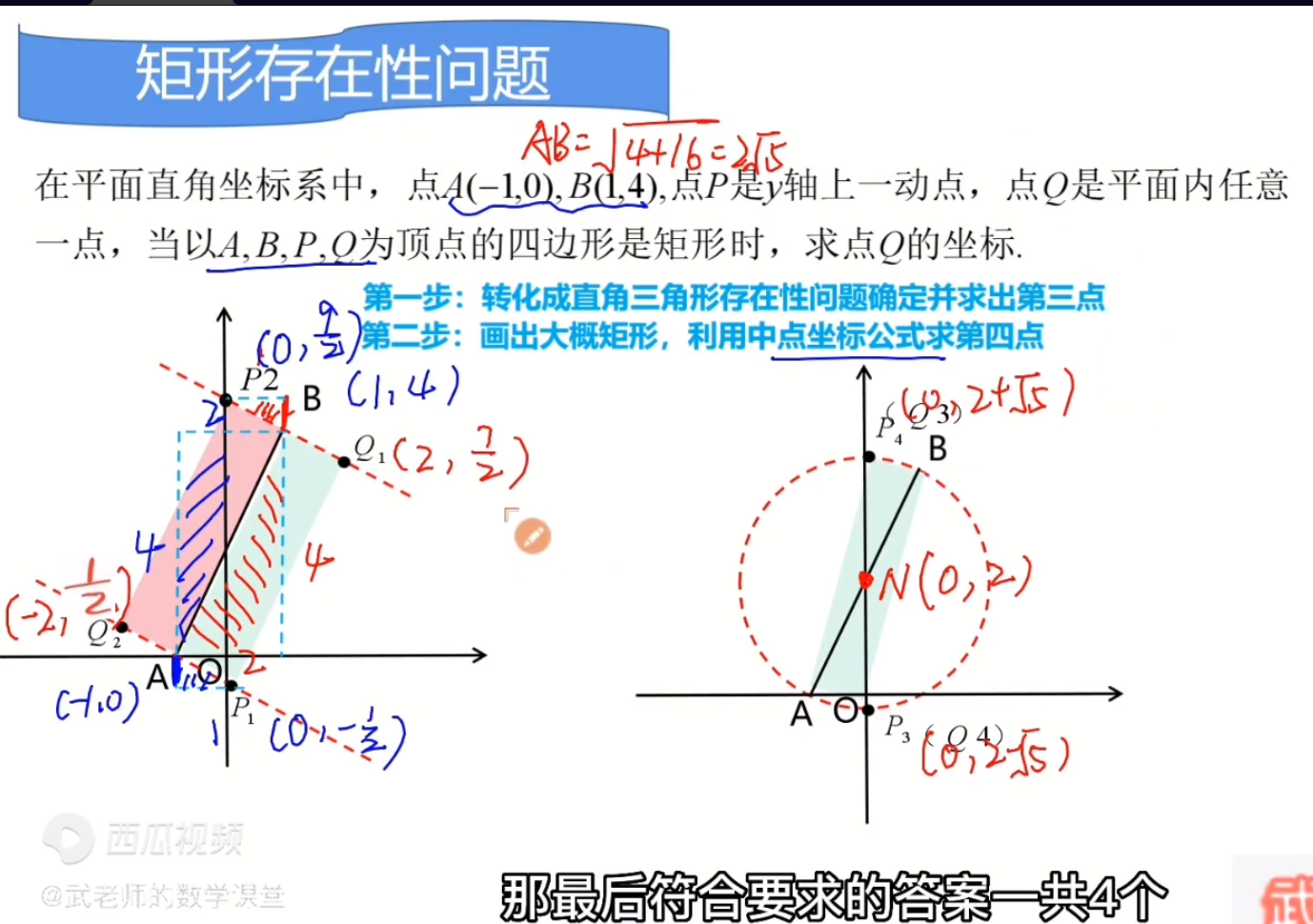
根据直角顶点的不同,应该有三种可能:
|
||
|
|
|
||
|
|
- $A$ 线
|
||
|
|
$\triangle ABH_1 \sim AOP$
|
||
|
|
$4:(1-(-1))=1:OP_1$
|
||
|
|
$OP_1=\frac{1}{2}$
|
||
|
|
$\therefore P_1(0,-\frac{1}{2})$
|
||
|
|
因为直角三角形是平行四边形,可以使用对角线的相关定理,$Q_x-1=1+0$
|
||
|
|
$\therefore Q_x=2$
|
||
|
|
$4+(-\frac{1}{2})=0+Q_y$
|
||
|
|
$\therefore Q_Y=\frac{7}{2}$
|
||
|
|
|
||
|
|
- $B$ 线
|
||
|
|
同理,$\triangle P_2H_2B \sim \triangle ABH_1$
|
||
|
|
根据比例关系,$P_2(0,\frac{9}{2})$
|
||
|
|
|
||
|
|
$$
|
||
|
|
\large \left\{\begin{matrix}
|
||
|
|
0-1=1+x & \\
|
||
|
|
\frac{9}{2}=4+y &
|
||
|
|
\end{matrix}\right. $$
|
||
|
|
|
||
|
|
解得:
|
||
|
|
$x=-2,y=\frac{1}{2}$
|
||
|
|
- $C$ 圆
|
||
|
|
|
||
|
|
|
||
|
|
先计算$A$B的距离=$\sqrt{4+16}=2\sqrt{5}$
|
||
|
|
半径就是$\sqrt{5}$
|
||
|
|
|
||
|
|
直线方程$y=kx+b,A(-1,0),B(1,4)$
|
||
|
|
$$
|
||
|
|
\large \left\{\begin{matrix}
|
||
|
|
-k+b=0 & \\
|
||
|
|
k+b=4 &
|
||
|
|
\end{matrix}\right. $$
|
||
|
|
$\therefore b=2,k=2$
|
||
|
|
方程$y=2x+2$
|
||
|
|
$N$点坐标可求:$N(0,2)$
|
||
|
|
|
||
|
|
$\therefore P_3(0,2+\sqrt{5}),P_4(0,2-\sqrt{5})$
|
||
|
|
|
||
|
|
此时发现,正好这两个点是矩形的另外两个坐标点,即$Q_1(0,2+\sqrt{5}),Q_2(0,2-\sqrt{5})$
|