You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
28 lines
1.2 KiB
28 lines
1.2 KiB
|
2 years ago
|
|
||
|
|
|
||
|
|
- 给出离的很远的两条边相等,就是让我们证明两个三角形全等:
|
||
|
|
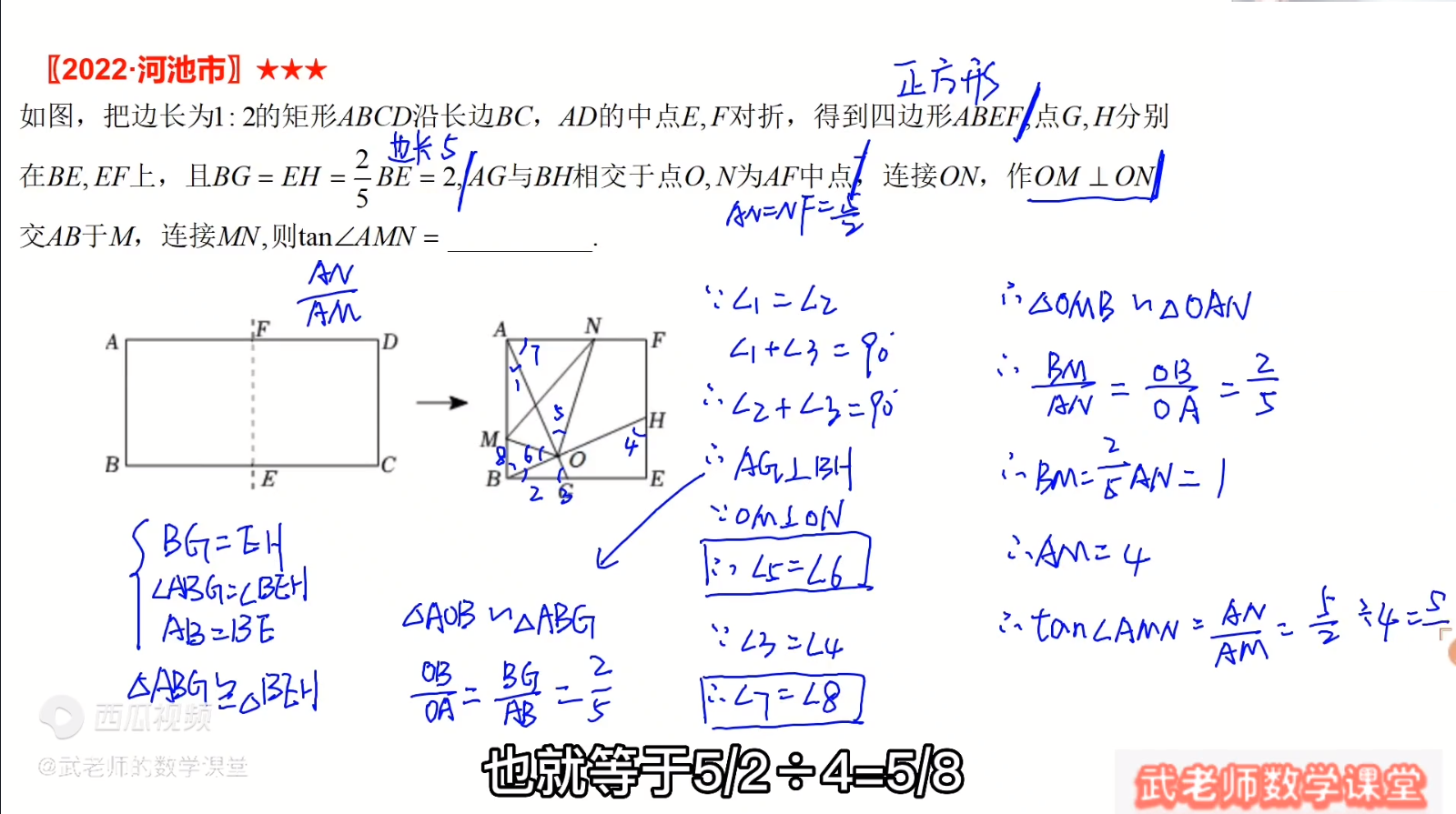
$\because BG=EH,\angle ABG=\angle BEH,AB=BE$
|
||
|
|
$\therefore \triangle ABG \cong \triangle BHE$
|
||
|
|
目的:
|
||
|
|
$\angle 1=\angle 2,\angle 3=\angle 4$
|
||
|
|
$\because \angle 1+\angle 3=90^{\circ},\angle 1=\angle 2 \Rightarrow \angle 2+\angle 3=90^{\circ}$
|
||
|
|
$\therefore \angle BOA=90^{\circ}$
|
||
|
|
|
||
|
|
- 这里有一个 **子母型** 的相似直角三角形:
|
||
|
|
$\triangle AOB \sim \triangle ABG$
|
||
|
|
$\therefore \frac{OB}{OA}=\frac{BG}{AB}=\frac{2}{5}$
|
||
|
|
|
||
|
|
因为知道$\triangle NOM$是直角三角形,所以应该是需要继续找出相似的直角三角形。
|
||
|
|
利用两个相交的直角,可以有$\angle AOM+\angle 5=\angle AOM+\angle 6$
|
||
|
|
$\therefore \angle 5=\angle 6$
|
||
|
|
$\because \angle 7=\angle 3,\angle 8=\angle 4$
|
||
|
|
|
||
|
|
$\because \angle 3=\angle 4$
|
||
|
|
$\therefore \angle 7=\angle 8$
|
||
|
|
|
||
|
|
$\therefore \triangle OMB \sim \triangle OAN$
|
||
|
|
$\therefore \frac{BM}{AN}=\frac{OB}{OA}=\frac{2}{5}$
|
||
|
|
$\therefore BM=\frac{2}{5}*\frac{5}{2}=1$
|
||
|
|
$\therefore AM=5-1=4$
|
||
|
|
$\therefore tan \angle AMN=\frac{AN}{AM}=\frac{5}{2} ÷ 4 =\frac{5}{8}$
|