You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
22 lines
865 B
22 lines
865 B
|
2 years ago
|
|
||
|
|
|
||
|
|
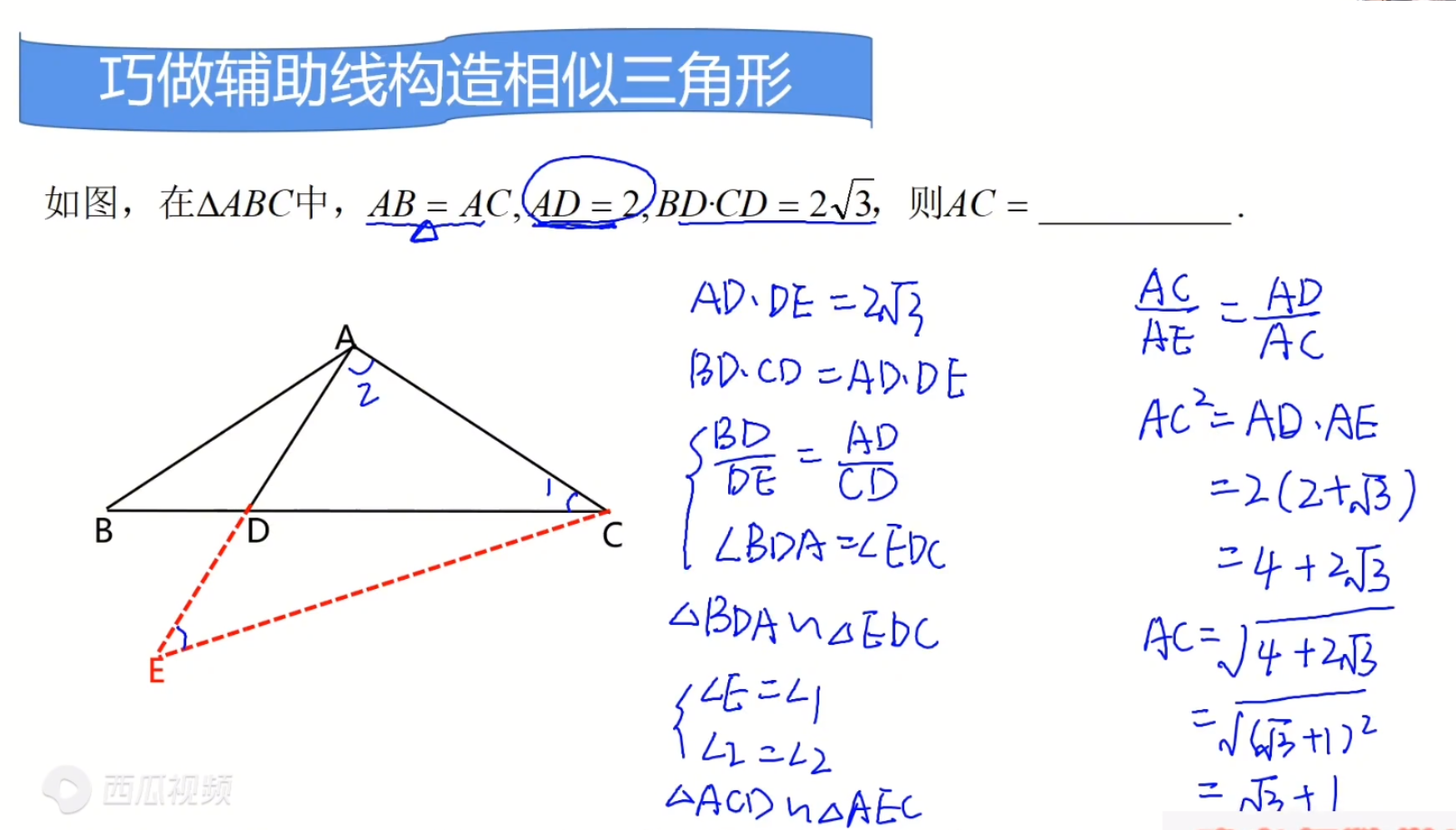
- 看到两条边的乘积,需要考虑相似三角形
|
||
|
|
- $BD \cdot CD=2\sqrt{3}$
|
||
|
|
如果这是在两个相似三角形中,那么可能需要延长$AD$,然后截取$DE$,使得$AD\cdot DE=BD \cdot DC$
|
||
|
|
|
||
|
|
$\because \frac{AD}{DC}=\frac{BD}{DE}$
|
||
|
|
再加上$\angle BDA=\angle EDC$
|
||
|
|
$\therefore \triangle ABD \sim \triangle EDC$
|
||
|
|
|
||
|
|
但是这样,好像离结果也没啥进展,还需要继续思考:
|
||
|
|
有一个结论:
|
||
|
|
$\angle AEC=\angle ABC=\angle 1$
|
||
|
|
<font color='red' size=4><b>母子相似三角形!</b></font>
|
||
|
|
$\because \angle 2=\angle 2$
|
||
|
|
$\because \angle CBA=\angle 1$
|
||
|
|
$\therefore \angle AEC=\angle 1$
|
||
|
|
$\triangle ACD \sim \triangle AEC$
|
||
|
|
|
||
|
|
$\therefore \frac{AC}{AE}=\frac{AD}{AC}$
|
||
|
|
将数值代入。解得:
|
||
|
|
$AC=\sqrt{3}+1$
|