You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
19 lines
970 B
19 lines
970 B
|
2 years ago
|
|
||
|
|
|
||
|
|
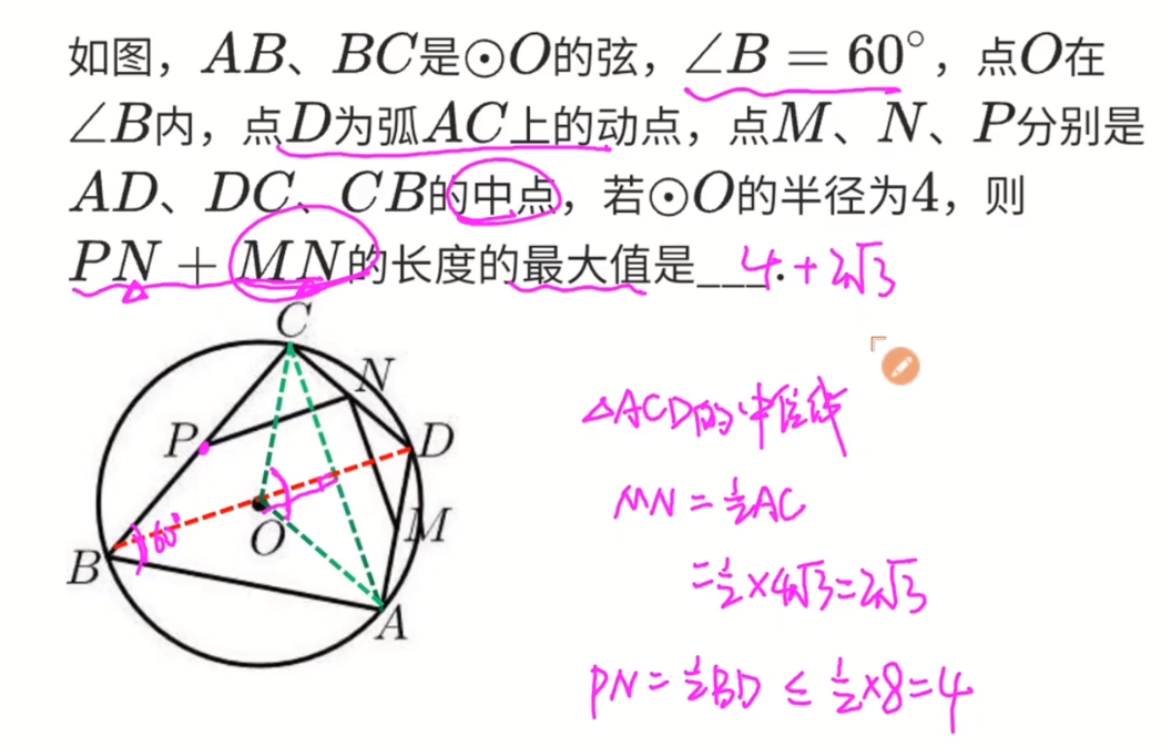
- 乍看似乎是 **有公共端点的最值问题**,这不是将军饮马问题吗?如果这样想,就错了!为什么呢?
|
||
|
|
|
||
|
|
因为将军饮马的模型,解决的是有公共端点的最小值问题,它现在问的是 **最大值**!
|
||
|
|
|
||
|
|
那怎么办呢?因为$M,N,P$三个点都中点,所以可以使用中位线来解决问题:
|
||
|
|
|
||
|
|
- $MN=\frac{1}{2}AC$
|
||
|
|
- $PN=\frac{1}{2}BD$
|
||
|
|
|
||
|
|
因为$A,B,C$都是固定点,只有$D$点是动点,所以$AC$长度是固定的,而$BD$是变化的。
|
||
|
|
|
||
|
|
$AC$很好求,因为$AC$在等腰三角形$AOC$中,而且$\angle AOC=120^{\circ}$
|
||
|
|
所以有结论:$AC=\sqrt{3}\times OA=4\sqrt{3}$
|
||
|
|
$\therefore MN=\frac{1}{2}OA=2\sqrt{3}$
|
||
|
|
|
||
|
|
而预求$PN+MN$最大值,就是求$PN$最大值,也就是求$\frac{1}{2}BD$
|
||
|
|
而$BD$最大值就是圆的直径$PN=\frac{1}{2}BD<=\frac{1}{2}\times 8=4$
|