14 KiB
【题型】不定项选择
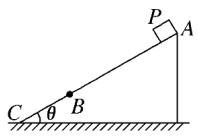
【题文】如图所示，固定斜面倾角为\theta，整个斜面分为AB、BC两段，AB{=}2BC.小物块P((可视为质点)与AB、BC两段斜面间的动摩擦因数分别为\mu_{1},\\mu_{2}.已知P由静止开始从A点释放，恰好能滑动到C点而停下，那么\theta、\mu_{1},\\mu_{2}间应满足的关系是( )
A．tan$\theta=\begin{array}{rl}{\mathrm{B}.}&{{}\tan\theta=}\end{array}C．\scriptstyle{\tan\theta=2\mu_{1}-\mu_{2}}\mathrm{~D~.~}\tan\theta{=}2\mu_{2}{-}\mu_{1}$
【答案】B
【解析】设斜面的长度为l，小物块从斜面顶端下滑到斜面底端的全过程由动能定理得：
mgl{\sin\theta}-{\mu}_{1}mg{\cos}{\theta}-{\mu}_{2}mg{\cos}{\theta}=0,，
解得\tan\theta=，故B正确
【知识点】动能定理
【难度】中
【题型】不定项选择
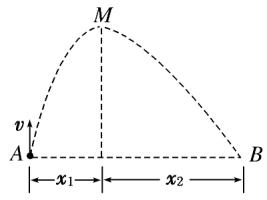
在有大风的情况下，一小球自A点竖直上抛，其运动轨迹如图9所示(小球的运动可看做竖直方向的竖直上抛运动和水平方向的初速度为零的匀加速直线运动的合运动)，小球运动轨迹上的A、B两点在同一水平直线上，M点为轨迹的最高点．若风力的大小恒定，方向水平向右，小球在A点抛出时的动能为4J，在M点时它的动能为2J，落回到B点时动能记为E_{\mathrm{k}B}，小球上升时间记为t_{1}，下落时间记为t_{2}，不计其他阻力，则()
A．x_{1}:x_{2}{=}1:3\qquad\mathrm{B}.\t_{1}{<}t_{2}$C．$E_{\mathrm{k}B}{=}6\mathrm{~J~}$D．$E_{\mathrm{k}B}=12~\mathrm{J}
【答案】AD
【解析】由小球上升与下落时间相等即t_{1}=t_{2}，
x_{1}:(x_{1}+x_{2})=1:2^{2}=1:4,
即x_{1}:x_{2}=1:3.A{}M应用动能定理得
-\mgh+{\calW}_{1}=m{v_{M}}^{2}\cdotmv^{2},，\enclose{circle}{1}
竖直方向有v^{2}=2gh\enclose{circle}{2}
\enclose{circle}{1}\enclose{circle}{2}式联立得W_{1}=2\\mathrm{J}
AB风力做功W_{2}=4W_{1}=8\mathrm{~J}，
AB由动能定理{\calW}_{2}=E_{\mathrm{k}B}-E_{\mathrm{k}A}，
可求得E_{\mathrm{k}B}=12~\mathrm{J}，A、D正确．
【知识点】运动学、动能定理
【难度】难
【题型】不定项选择
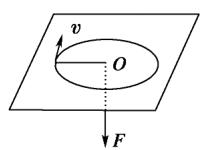
如图所示，一个质量为m的圆环套在一根固定的水平长直杆上，环与杆的动摩擦因数为\mu.现给环一个向右的初速度v_{0}，同时对环施加一个竖直向上的作用力F，并使F的大小随环的速度的大小变化，两者关系为F{=}kv，其中k为常数，则环在运动过程中克服摩擦所做的功的大小不可能为( )
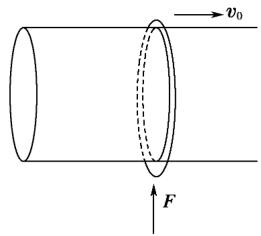A.B．0C.＋D.－
【答案】C
【解析】若圆环最终静止，则－{\calW}_{f}=0-\,~{\calW}_{f}=\,，A可能；若圆环刚开始运动时，mg=F=kv_{0}，圆环一直做匀速运动，克服摩擦所做的功为零，B可能；若圆环最终做匀速运动，mg=F=kv，v=，则－{\calW}_{f}=\.－，化简得W_{f}={\mathrm{~~\bar{~}{~\bf~,~}~}}\mathrm{~D~}可能，C不可能．
【知识点】物体的平衡、牛顿第二定律、动能定理
【难度】中
【题型】不定项选择
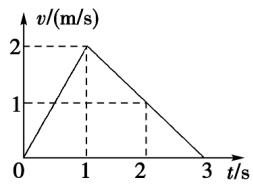
物体在合外力作用下做直线运动的v-t图象如图所示．下列表述正确的是( )
A．在0{\sim}2\mathrm{s}内，合外力总是做负功B．在1\sim2\mathrm{s}内，合外力不做功C．在0\sim3\mathrm{s}内，合外力做功为零D．在0\sim1\mathrm{s}内比1{\sim}3\mathrm{s}内合外力做功快
【答案】CD
【解析】根据物体的速度图象和动能定理可知在0\sim2s内物体先加速后减速，合外力先做正功后做负功，A错；根据动能定理得0\sim3\mathrm{s}内合外力做功为零，1\sim2\mathrm{s}内合外力做负功，
C对，B错；在0\sim1{\mathrm{s}}内比1\sim3\mathrm{s}内合外力做功快，D对．【知识点】v-t图像、动能定理
【难度】易
【题型】不定项选择
如右图所示，质量为m的物体用细绳经过光滑小孔牵引在光滑水平面上做匀速圆周运动，拉力为某个值F时，转动半径为R，当拉力逐渐减小到时，物体仍做匀速圆周运动，半径为2R，则外力对物体所做的功大小是( )
A.B.C.D．0
【答案】A
【解析】设当绳的拉力为F时，小球做匀速圆周运动时线速度为v_{1}，则有F=m
当绳的拉力减为时，小球做匀速圆周运动的线速度为v_{2}，则有
F=m
在绳的拉力由F减为F的过程中，绳的拉力所做的功为
W{=}m{v_{2}}^{2}\cdotm{v_{1}}^{2}{=}\cdotFR
所以，绳的拉力所做功的大小为FR.
【知识点】圆周运动、动能定理
【难度】易
【题型】计算题
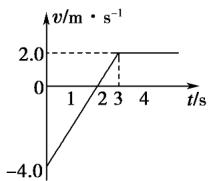
一质量为M{=}2.0\mathrm{kg}的小物块随足够长的水平传送带一起向右匀速运动，被一水平向左飞来的子弹击中，且子弹从小物块中穿过，子弹和小物块的作用时间极短，如图甲所示．地面观察者记录的小物块被击中后的速度随时间变化关系如图乙所示(图中取向右运动的方向为正方向)．已知传送带的速度保持不变，g取10\mathrm{m}/\mathrm{s}^{2}.求：
图甲
图乙
(1)传送带的速度v的大小；(2)小物块与传送带之间的动摩擦因数\mu；(3)传送带对小物块所做的功
【答案】(1)2.0\mathrm{m}/\mathrm{s}(2)0.2(3)－12J
【解析】(1)小物块最后与传送带的运动速度相同，从图象上可读出传送带的速度v的大
小为2.0\mathrm{m}/\mathrm{s}
(2)由速度图象可得，小物块在滑动摩擦力的作用下做匀变速运动的加速度为a=\Deltav/\Deltat=2.0\mathrm{m}/\mathrm{s}^{2}
由牛顿第二定律得f=\muMg=Ma
得到小物块与传送带之间的动摩擦因数\mu==0.2
(3)从子弹离开小物块到小物块与传送带一起匀速运动的过程中，设传送带对小物块所做的功为W，由动能定理得：
{\calW}=\DeltaE_{\mathrm{k}}=\-
从速度图象可知：v_{\mathrm{1}}=4.0\mathrm{m/s}v_{2}=v=2.0\mathrm{m/s}
解得：W=\textrm{-}12\mathrm{J}.
【知识点】牛顿第二定律、v-t图像、定能定理
【难度】中
【题型】计算题
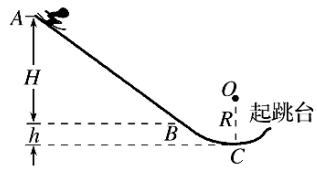
我国将于2022年举办冬奥会，跳台滑雪是其中最具观赏性的项目之一．如图所示，质量m=60\mathrm{kg}的运动员从长直助滑道AB的A处由静止开始以加速度a{=}3.6\\mathrm{m/s^{2}}匀加速滑下，到达助滑道末端B时速度v_{B}{=}24\mathrm{m/s}，A与B的竖直高度差H{=}48\mathrm{m}，为了改变运动员的运动方向，在助滑道与起跳台之间用一段弯曲滑道衔接，其中最低点C处附近是一段以O为圆心的圆弧．助滑道末端B与滑道最低点C的高度差h{=}5\mathrm{~m~}，运动员在B、C间运动时阻力做功W{=}{-}1530\mathrm{~J}，取g{=}10\mathrm{m}/\mathrm{s}^{2}.
(1)求运动员在AB段下滑时受到阻力F_{\mathrm{f}}的大小；
(2)若运动员能够承受的最大压力为其所受重力的6倍，则C点所在圆弧的半径R至少应为多大．
【答案】(1)144N(2)12.5m
【解析】(1)运动员在AB上做初速度为零的匀加速运动，设AB的长度为x，则有\boldsymbol{v}=2ax(1)
由牛顿第二定律有mg\textrm{-}F_{\mathrm{f}}=ma\enclose{circle}{2}
联立\enclose{circle}{1}\enclose{circle}{2}式，代入数据解得F_{\mathrm{f}}=144\mathrm{N}\enclose{circle}{3}
(2)设运动员到达C点时的速度为v_{C}，在由B到达C的过程中，由动能定理得
mgh+W=mv\–\mv\enclose{circle}{4}
设运动员在C点所受的支持力为F_{\mathrm{N}}，由牛顿第二定律有
F_{\mathrm{N}}-mg=m\enclose{circle}{5}
由题意和牛顿第三定律知F_{\mathrm{N}}=6mg\enclose{circle}{6}
联立\enclose{circle}{4}\enclose{circle}{5}\enclose{circle}{6}式，代入数据解得
R=12.5\\mathrm{m}.
【知识点】圆周运动、动能定理、牛顿第二定律、运动学
【难度】中
【题型】计算题
如图所示为某游乐场内水上滑梯轨道示意图，整个轨道在同一竖直平面内，表面粗糙的AB段轨道与四分之一光滑圆弧轨道BC在B点水平相切．点A距水面的高度为H，圆弧轨道BC的半径为R，圆心O恰在水面．一质量为m的游客(视为质点)可从轨道AB的任意位置滑下，不计空气阻力
(1)若游客从A点由静止开始滑下，到B点时沿切线方向滑离轨道落在水面D点，OD=2R，求游客滑到B点时的速度v_{B}大小及运动过程轨道摩擦力对其所做的功W_{\mathrm{f}}{\mathrm{;}}；(2)某游客从AB段某处滑下，恰好停在B点，又因受到微小扰动，继续沿圆弧轨道滑到P点后滑离轨道，求P点离水面的高度h.(提示：在圆周运动过程中任一点，质点所受的向心力与其速率的关系为F_{\mathrm{\scriptsize~[H}}=m)
【答案】(1)-(mgH-2mgR)~(2)R
【解析】(1)游客从B点做平抛运动，有
\begin{array}{l}{2R=v_{B}t\enclose{circle}{1}}\\{~R=gt^{2}\enclose{circle}{2}}\end{array}
由\enclose{circle}{1}\enclose{circle}{2}式得v_{B}=\enclose{circle}{3}
从A到B，根据动能定理，有
mg(H-R)+W_{\mathrm{f}}=mv-0\enclose{circle}{4}由\enclose{circle}{3}式得W_{\mathrm{f}}=\mathrm{~-~}(mgH-2mgR)
(2)设OP与OB间夹角为\theta，游客在P点时的速度为v_{P}，受到的支持力为N，从B到P由机械能守恒定律，有
mg(R\textrm{-}R\cos\theta)=mv\textrm{-}0\enclose{circle}{5}
过P点时，根据向心力公式，有
mgcos$\theta-N=m\enclose{circle}{6}$
N=0\enclose{circle}{7}
cos$\theta=\enclose{circle}{8}$
由\enclose{circle}{5}\enclose{circle}{6}\enclose{circle}{7}\enclose{circle}{8}式解得h=R.
【知识点】圆周运动、动能定理、牛顿第二定律、平抛运动
【难度】难
【题型】计算题
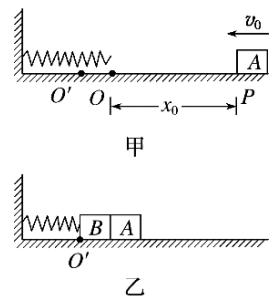
如图甲所示，轻弹簧左端固定在竖直墙上，右端点在O位置．质量为m的物块A(可视为质点)以初速度v_{0}从距O点右方x_{0}处的P点向左运动，与弹簧接触后压缩弹簧，将弹簧右端压到O^{\prime}′点位置后，A又被弹簧弹回．A离开弹簧后，恰好回到P点．物块A与水平面间的动摩擦因数为\mu..求：
(1)物块A从P点出发又回到P点的过程，克服摩擦力所做的功
(2)O点和O^{\prime}′点间的距离x_{1}.
(3)如图乙所示，若将另一个与A完全相同的物块B((可视为质点)与弹簧右端拴接，将A放在B右边，向左推A,\B，使弹簧右端压缩到O^{\prime}′点位置，然后从静止释放，A、B共同滑行一段距离后分离．分离后物块A向右滑行的最大距离x_{2}是多少？
【答案】\mid(1)mv(2)-x_{0}(3)x_{0}-
【解析】(1)物块A从P点出发又回到P点的过程，根据动能定理得克服摩擦力所做的功为W_{\mathrm{f}}=mv.
(2)物块A从P点出发又回到P点的过程，根据动能定理得
2\mumg(x_{1}+x_{0})=mv
解得x_{1}=\mathbf{\nabla}-x_{0}
(3)A、B在弹簧处于原长处分离，设此时它们的共同速度是v_{1}，弹出过程弹力做功为W_{F}只有A时，从O^{\prime}′到P有
W_{F}-\mumg(x_{1}+x_{0})=0~-~0
A、B共同从O^{\prime}到O有
W_{F}-2\mumgx_{1}=\times2mv
分离后对A有mv=\mumgx_{2}
联立以上各式可得x_{2}=x_{0}\\cdot.
【知识点】动能定理【难度】中
【题型】计算题
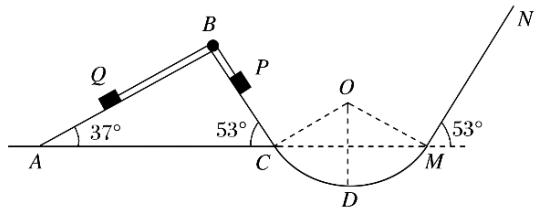
如图所示，半径R{=}0.5~\mathrm{m}的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点，斜面倾角分别如图所示．O为圆弧圆心，D为圆弧最低点，C,\M在同一水平高度．斜面体ABC固定在地面上，顶端B安装一定滑轮，一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、\mathcal{Q}((两边细绳分别与对应斜面平行)，并保持P、\mathcal{Q}两物块静止．若PC间距为L_{1}{=}0.25~\mathrm{m}，斜面MN足够长，物块P的质量m_{\mathrm{l}}{=}3~\mathrm{kg}，与MN间的动摩擦因数\mu=，重力加速度g{=}10\mathrm{m}/\mathrm{s}^{2}，求：(\sin37^{\circ}=0.6，cos$37^{\circ}{=}0.8$)
(1)小物块\mathcal{Q}的质量m_{2}；
(2)烧断细绳后，物块P第一次到达D点时对轨道的压力大小；(3)物块P在MN斜面上滑行的总路程
【答案】(1)4\mathrm{kg}(2)78N(3)1.0m
【解析】(1)根据共点力平衡条件，两物块的重力沿斜面的分力相等，有：m_{1}g\sin53^{\circ}=m_{2}g\sin37^{\circ}
解得：m_{2}=4\mathrm{kg}
即小物块Q的质量m_{2}为4\mathrm{kg}.
(2)小物块P第一次到达D点过程，由动能定理得m_{1}gh=m_{1}v
根据几何关系，有：
h=L_{1}\mathrm{sin}53^{\circ}+R(1-\cos53^{\circ})
在D点，支持力和重力的合力提供向心力：F_{D}-m_{1}g=m_{1}
解得：F_{D}=78\mathrm{N}
由牛顿第三定律得，物块P对轨道的压力大小为78\mathrm{N}.
(3)分析可知最终物块在CDM之间往复运动，C点和M点速度为零．由全过程动能定理得：m_{1}gL_{1}\mathrm{sin}53^{\circ}-\mum_{1}g\mathrm{cos}53^{\circ}L\mathrm{s}=0
解得L_{☉}=1.0\:\mathrm{m}
即物块P在MN斜面上滑行的总路程为1.0\mathrm{m}.
【知识点】物体的平衡、动能定理、牛顿第二定律
【难度】难