2.6 KiB
2.6 KiB
超多数学动画:高中、初中、小学!动态数学软件GeoGebra教程汇总
https://www.toutiao.com/article/6994257361020109316
Q:矩形、直角三角形、直角梯形、半圆分别绕其一条边、一条直角边、一条高、一条直径所在直线,旋转一周,会形成什么几何体呢?
www.ggb123.cn
啊K数学 https://www.geogebra.org/u/%E5%95%8Ak%E6%95%B0%E5%AD%A6
序列法脚本
# 构造三维坐标的矩形
q1 = Polygon((0, 0, 0), (1, 0, 0), (1, 0, 3), (0, 0, 3))
# 创建滑动条:
α = Slider(0°, 360°)
# 至于将矩形旋转一周,可当做是逐渐产生一系列绕着z轴的矩形
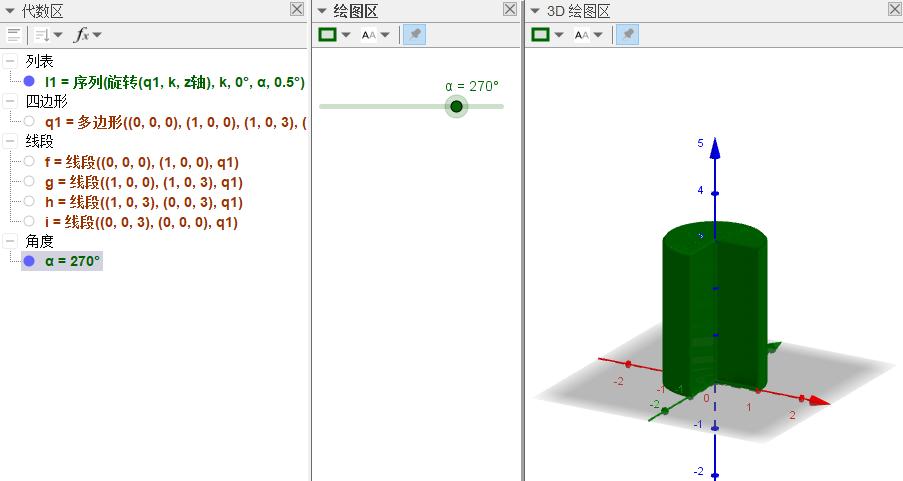
l1 = Sequence(Rotate(q1, k, zAxis), k, 0°, α, 0.5°)
#拉动滑动条α,即有将矩形旋转一周,生成圆柱的效果。
这条命令是 GeoGebra 中用于生成旋转矩形序列的关键语句,让我为您详细解释:
l1 = Sequence(Rotate(q1, k, zAxis), k, 0°, α, 0.5°)
分解说明:
Sequence()函数 这是序列生成函数,用于创建按特定规律排列的对象集合Rotate(q1, k, zAxis)q1: 要旋转的原始矩形(之前定义的多边形)k: 旋转角度变量(单位:度°)zAxis: 旋转轴(Z轴)- 作用:将矩形 q1 绕 Z 轴旋转 k 度
- 参数序列
k, 0°, α, 0.5°k: 循环变量0°: 起始角度α: 结束角度(由滑动条控制)0.5°: 角度增量步长
完整含义:
"创建名为 l1 的序列,该序列包含将矩形 q1 绕 Z 轴从 0° 到 α° 旋转的所有矩形副本,旋转角度以 0.5° 为间隔逐步增加"
动态效果:
当您拖动滑动条 α 时:
- α=0° → 序列包含 1 个矩形(未旋转)
- α=90° → 序列包含 180 个矩形(0°,0.5°,1°...90°)
- α=360° → 序列包含 720 个矩形(0° 到 360° 每 0.5° 一个)
几何意义:
这些紧密排列的旋转矩形(间隔仅 0.5°)在视觉上会形成连续的圆柱面,这就是注释中说的"生成圆柱的效果"。本质上是通过离散旋转逼近连续旋转曲面。