98 lines
4.8 KiB
Markdown
98 lines
4.8 KiB
Markdown
> 1\.
|
||
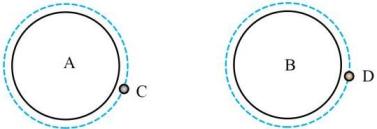
> 《天问》是屈原笔下的不朽诗篇,而"天问"行星探索系列代表着中国人对深空物理研究的不懈追求。如下图所示,半径均为R的两球形行星A、B的密度之比为
|
||
> 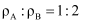
|
||
> ,A、B各有一个近地卫星C、D,其绕行周期分别为:
|
||
> 
|
||
> 、
|
||
> 
|
||
> 。站在行星表面的宇航员从距A行星表面高为h处以
|
||
> 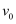
|
||
> 水平抛出一物体a,从距B行星表面高为2h处以
|
||
> 
|
||
> 水平抛出另一物体b。下列说法正确的是( )
|
||
>
|
||
> 
|
||
>
|
||
>
|
||
> A. C、D绕A、B运行的速度之比为
|
||
> 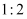
|
||
>
|
||
>
|
||
> B. B、D绕A、B运行的周期满足
|
||
> 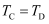
|
||
>
|
||
>
|
||
> C. 由于不知道a与b的质量,所以无法求出二者落地时速度之比
|
||
>
|
||
> D. a、b两物体从抛出到落地的位移之比为
|
||
> 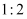
|
||
>
|
||
>
|
||
> 【难度】\
|
||
> 中等
|
||
>
|
||
> 【答案】
|
||
>
|
||
> D
|
||
>
|
||
> 【解析】
|
||
>
|
||
> 【解答】由于两个行星半径相等则体积相等,根据密度公式可以得出星球A和B的质量之比为\
|
||
> \
|
||
> 
|
||
> \
|
||
> \
|
||
> 根据引力提供向心力可以得出两个近地卫星的周期的表达式为\
|
||
> \
|
||
> 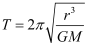
|
||
> \
|
||
> \
|
||
> 所以两个近地卫星的周期之比为\
|
||
> \
|
||
> 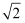
|
||
> :1\
|
||
> \
|
||
> 根据线速度的表达式为\
|
||
> \
|
||
> 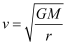
|
||
> \
|
||
> \
|
||
> 则可以得出两个近地卫星的线速度之比为\
|
||
> \
|
||
> 1:
|
||
> 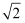
|
||
> \
|
||
> \
|
||
> 根据引力形成重力可以得出\
|
||
> \
|
||
> 
|
||
> \
|
||
> \
|
||
> 则两个抛出物体的重力加速度之比为为:1:2,根据位移公式\
|
||
> \
|
||
> 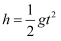
|
||
> \
|
||
> \
|
||
> 可以求出运动的时间之比为:1:1;则根据水平方向的位移公式可以求出运动的水平位移之比为1:2;则合位移之比为1:2;根据速度公式可以求出落地竖直方向的速度之比为1:1,则根据速度的合成\
|
||
> \
|
||
> 
|
||
> \
|
||
> \
|
||
> 未知分速度的关系不能求出合速度的比值,所以ABC错误,D对;\
|
||
> \
|
||
> 正确答案为D。\
|
||
> \
|
||
> 【分析】利用引力提供向心力结合行星质量的大小可以求出线速度和周期的比值;利用引力形成重力可以求出重力加速度的比值,结合位移公式可以求出平抛运动的时间之比,结合速度的合成可以求出合速度的比值;利用位移的合成可以求出合位移的比值。
|
||
>
|
||
> 【关联章节】第七章 万有引力与宇宙航行第七章 万有引力与宇宙航行 \> 2.
|
||
> 万有引力定律第七章 万有引力与宇宙航行 \> 3. 万有引力理论的成就;
|
||
>
|
||
> 【关联知识点】经典力学的成就与局限性 \>
|
||
> 万有引力定律经典力学的成就与局限性 \>
|
||
> 万有引力定律的适用条件经典力学的成就与局限性 \>
|
||
> 万有引力定律的应用相互作用与运动规律;
|
||
>
|
||
> 【关联素养点】暂无数据
|
||
>
|
||
> 【关联关键能力】暂无数据
|