1.1 KiB
1.1 KiB
【题型】不定项选择
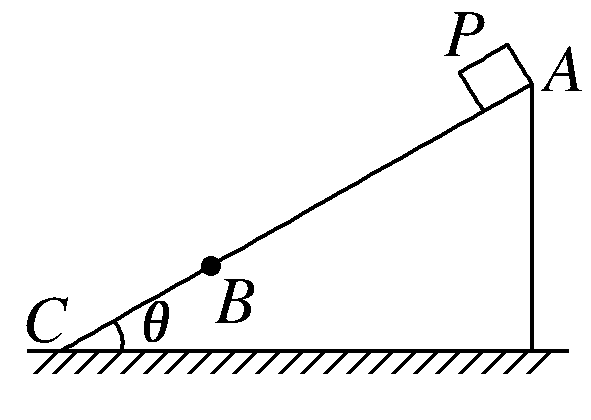
【题文】如图所示,固定斜面倾角为θ,整个斜面分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,那么θ、μ1、μ2间应满足的关系是( )
 {width="0.9847222222222223in"
height="0.6979166666666666in"}A.
{width="0.9847222222222223in"
height="0.6979166666666666in"}A.tan\theta\text{=}\frac{\mu_{1} + 2\mu_{2}}{3}
B.tan\theta\text{=}\frac{2\mu_{1} + \mu_{2}}{3}
C.tan\theta\text{=}2\mu_{1} - \mu_{2}
D.tan\theta\text{=}2\mu_{2} - \mu_{1}
【答案】 B
【解析】设斜面的长度为l,小物块从斜面顶端下滑到斜面底端的全过程由动能定理得:
mglsin\theta\text{-}\mu_{1}mg\frac{2l}{3}cos\theta\text{-}\mu_{2}mg\frac{l}{3}cos\theta\text{=}0
解得$tan\theta\text{=}\frac{2\mu_{1} + \mu_{2}}{3}$,故B正确. 【知识点】动能定理 【难度】中