84 lines
4.3 KiB
Markdown
84 lines
4.3 KiB
Markdown
> 1\.
|
||
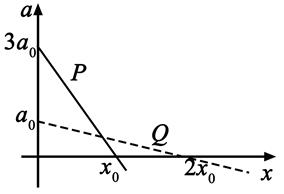
> 在星球M上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示。在另一星球N上用完全相同的弹簧,改用物体Q完成同样的过程,其a--x关系如图中虚线所示,假设两星球均为质量均匀分布的球体。已知星球M的半径是星球N的3倍,则(
|
||
> )
|
||
>
|
||
> 
|
||
>
|
||
>
|
||
> A. M与N的密度相等
|
||
>
|
||
> B. Q的质量是P的3倍
|
||
>
|
||
> C. Q下落过程中的最大动能是P的4倍
|
||
>
|
||
> D. Q下落过程中弹簧的最大压缩量是P的4倍
|
||
>
|
||
> 【难度】\
|
||
> 难
|
||
>
|
||
> 【答案】
|
||
>
|
||
> A,C
|
||
>
|
||
> 【解析】
|
||
>
|
||
> 【解答】把物体P轻放在弹簧上端,一开始,弹簧尚未变形,物体仅受重力作用,由图像可知这时物体P的加速度为3a~0~
|
||
> , 根据牛顿第二定律知:
|
||
> 
|
||
> ,同理
|
||
> 
|
||
> 。由万有引力公式知:
|
||
> 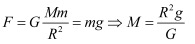
|
||
> ,
|
||
> 
|
||
> ,
|
||
> 
|
||
> ,故A正确;
|
||
>
|
||
> 当物体的加速度为零时,物体受力平衡,这时
|
||
> 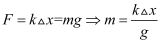
|
||
> ,
|
||
> 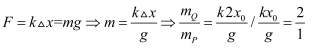
|
||
>
|
||
>
|
||
> 故B错误。
|
||
>
|
||
> 起初,物体P做加速度逐渐减小的加速运动,当物体的加速度为零时,速度最大,动能最大,因物体运动整个过程只受到弹力和重力作用,故机械能守恒,设初始状态机械能为零,对P:
|
||
> 
|
||
>
|
||
>
|
||
> 
|
||
> ,
|
||
> 
|
||
> 故
|
||
> 
|
||
>
|
||
> ,故C正确。当速度为零时,弹簧的压缩量最大,由机械能守恒知:
|
||
>
|
||
> 对P:
|
||
> 
|
||
>
|
||
>
|
||
> 对Q:
|
||
> 
|
||
> ,故
|
||
> 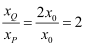
|
||
> ,故D错。
|
||
>
|
||
> 故AC正确,BD错误。
|
||
>
|
||
> 故答案为:AC
|
||
>
|
||
> 【分析】弹簧尚未变形前,物体仅受重力作用,据此求出星球的重力加速度。根据星球表面万有引力和重力相等,求星球质量,代入密度公式求密度比即可。物体运动整个过程只受到弹力和重力作用,故机械能守恒,根据机械能相等分别列式求出最大动能。当速度为零时,弹簧的压缩量最大,同样根据机械能守恒分别列式计算比较。
|
||
>
|
||
> 【关联章节】第七章 万有引力与宇宙航行第八章 机械能守恒定律第七章
|
||
> 万有引力与宇宙航行 \> 2. 万有引力定律第八章 机械能守恒定律 \> 4.
|
||
> 机械能守恒定律;
|
||
>
|
||
> 【关联知识点】热力学定律与能量守恒 \> 功和内能经典力学的成就与局限性
|
||
> \> 万有引力定律机械能和能源 \> 机械能守恒定律;
|
||
>
|
||
> 【关联素养点】暂无数据
|
||
>
|
||
> 【关联关键能力】暂无数据
|